Chem 260H Exploration 3: Rate Laws
Introduction
Thermodynamics is able to explain in what direction a chemical reaction will proceed, yet it provides no information on how quickly a reaction proceeds. For example, thermodynamic concepts like Gibbs free energy provide no information on how fast a reaction will proceed. The decomposition of diamond into graphite is thermodynamically favored, yet we have never seen a diamond ring change like that. Thus, we need to go beyond thermodynamics to explain why the transition from diamond to graphite is so slow. Kinetics fills in this conceptual gap by explaining how fast a reaction proceeds, and in the meantime, the mechanism of the reaction can be elucidated.
Reaction Rate Laws
Due to chemical equilibrium, we can state that any reaction can proceed either forwards or backwards. However, oftentimes we notice that the reverse reaction is relatively negligible, therefore the rate that gets analyzed is in the forward direction , or products → reactants.
A rate law, also know as an empirical rate expression , shares the relationship between the reaction rate and the concentration and features the proportionality constant, k. The rate laws, as well as the proportionality constant and its units, vary based on reaction order. For instance, in a first order reaction, the rate law will look something like rate=k[product]n where n is equal to 1 while in a zeroth order reaction the rate is simply equal to k.
Empirical and Integrated Rate Laws
Common rate laws are determined based on how the concentration of a reactant affects the rate of a reaction. The general expression for a rate law is shown below:

In the equation, R is the rate of reaction, k is the rate constant, and the bracket quantity [X] is the concentration of a reactant. [1]
It turns out that the powers in the formula often depend on the stoichiometry of the reaction, which occurs in reactions without intermediates. Elementary reactions are reactions without intermediates, from which all complex reactions can be built off from [2]. Understanding the rate laws of elementary reactions will allow us to understand the rates of complex reactions.
Rate Law Formulas
For reactions without intermediates, the general rate law equation (shown below) corresponds to the following reaction, where A and B are the reactants, with the stoichiometric coefficients a and b, respectively [1]:

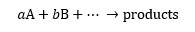
Note that in the rate law fomula, the overall reaction order is the sum of the stoichiometric coefficients. We will now focus on reactions involving a unique reactant. The rate law now becomes:

From this expression alone, the concentration of the reactant A as a function of time can be determined using Calc I skills (see http://chemwiki.ucdavis.edu/Physical_Chemistry/ Kinetics/Rate_Laws/The_Rate_Law for a full derivation of all the rate laws discussed).
When finding the relationship between the concentration of reactant and the time of the reaction, the half life can also be found, which is the time at which half of the reactant has been used up in the reaction.
-
Zeroth order reaction
If the change in the concentration of reactant A is unaffected by the concentration of A, then the concentration of A will change linearly over time: [1]
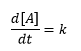
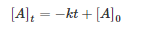
 [1]
[1]
Concentration of A over time: [3]
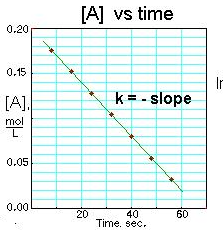
-
First order reaction
If the change in the concentration of reactant A is directly proportional to the concentration of A, then the concentration of A will change logarithmically over time: [1]

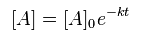
 [1]
[1]
Concentration of A over time: [3]
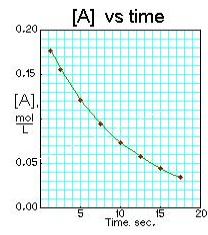
-
Second order reaction
If the change in the concentration of reactant A is dependent on the square of the concentration of A, then the concentration of A will change linearly over time: [1]
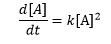

 [1]
[1]
Concentration of A over time: [3]

What do Rate Laws Depend on?
For rate laws, the reaction rate is affected by the concentration of reactants, concentration of products, mechanism of the reaction, and time. These factors are seen from the general relationship between products, reactants, and reaction coefficients in a reaction. If a general reaction for is a A + b B → c C + d D then the use or formation of each molecule or element occurs at the same rate. This makes sense because the formation of the products depends on the use of the reactants. Therefore the following relationship holds true :
-1/a dA/dt = -1/b dB/dt = 1/c dC/dt = 1/d dD/dt
This dependence on concentration of reactants, concentration of products, mechanism of reaction, and time allows scientists discover information about the type of reaction solely from the different rates. As you can see in the figure below, the green reaction is very different than the orange reaction. The green reaction rate increases rapidly almost to a vertical line. This means the concentration of the product is increasing faster than the environment can respond which is an indicator of a reaction that results in an explosion [9]. Alternately the orange reaction rate increases over time initially and then stabilizes. This graph is an example of a reaction that results a saturation.
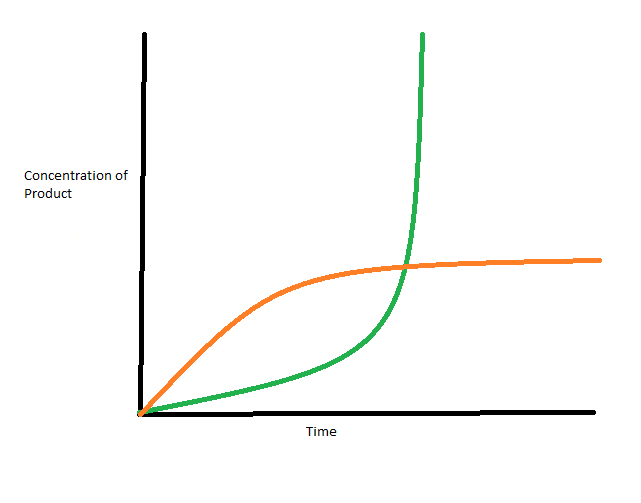
Multistep Reaction
Certain reactions occur in a series of products and intermediates. These multistep reactions have various reactions within them leading to multiple steps. These steps each have individual rates making the slowest reaction in this series the rate-determining step. The rate-determining step is critical in scientific research because the reaction can logically occur only as fast as the slowest step.
If the rate determining step is the first step, the reaction rate law is equal to the rate law of the slowest step and the remaining are negligible[5], since the fast steps can be assumed to come to equilibrium. However, reactions that have rate-determining steps that occur after one or more fast steps, have rate laws that account for the fast steps as well.
Example:

The overall rate law is given by the slowest step or step 2. Therefore the rate can be given by rate= k2 [I-][OCl]. However, this problem is slightly more complex due to the equilibrium for step 1 which complicates the situation since HOCl is at equilibrium with the reactants of step 1 which must be taken into consideration. Creating a new constant K1which is equal to k1/k-1 which in turn equals [HOCl] [OH-] / [OCl-]. Solving for both shows the rate of the overall reaction as rate = k2K1[I-] [OCl-] / [OH-] .
Transition States, Activation Energy, and the Rate Constant
The foundation of kinetics rests on the transition state, which is the intermediate, reactive species found during a reaction [7]. The transition state is important for kinetics, since the active energy, which is energy difference between the transition state and the reactants, is a factor in determining the rate constant in the Arrhenius equation. (The double dagger next to the transition state molecule is the convention for labelling a molecule as a transition state.)
 [7]
[7]
The rate constant k, gives information on how fast the reaction proceeds. The speed of a reaction depends on the activation energy, that is, the energy for the transition state to be formed. It is represented as Eain the below graph [6]:

Since the speed of the reaction depends on the activation energy, then more thermal energy in the environment will speed up reactions as more energy is available to achieve the transition state of a reaction. We can relate temperature and activation energy in the Arrhenius equation:
 [8]
[8]
The frequency factor takes into account of how probable it is for molecules to achieve the transition state [6].
Questions:
1. Which rate law is independent of concentration?
A. Zero Order
B. First Order
C. Second Order
D. None, all rate laws are dependent on concentration
2. Rate laws can be extended to other systems beside chemical reactions. Carbon-14, used to date items within the last 100,000 years, decays with a half life of 5730 years to carbon-12 [4]. The half-life of the carbon-14 is independent of the original amount of carbon-14 in a sample, which is a huge benefit of using carbon dating. What is the rate constant for the decay C14 → C12
A. Zero order, since the rate of carbon-14 decay is independent of the concentration of carbon-14.
B. First order, since the half-life of carbon-14 decay is independent of carbon-14 concentration.
C. Second order, since carbon-14 decays into two carbon-12 atoms.
D. First order, since the rate of carbon-14 decay is independent of the concentration
of carbon-14.
3. A catalyst lowers the activation energy of a reaction. Which of the following statements are true?
A. The rate constant is higher for a catalyzed reaction, thus increasing the rate at which the reaction proceeds. So the rate constant is lower for uncatalyzed reactions.
B. The rate constant is dependent on temperature, and since catalysts lower the temperature of a reaction, the rate constant is lower.
C. The rate constant decreases for a catalyzed reaction, thus decreasing the rate of the reaction.
D. Some of the above.
E. None of the above.
4. A reaction gave the following graph for the rate of product formation over time. Do you want to be near this reaction?
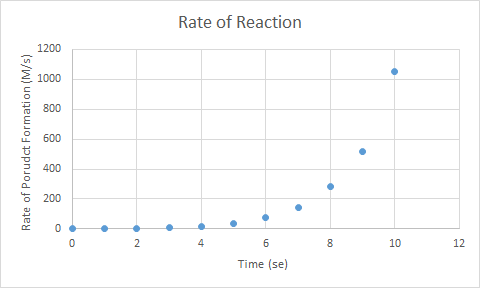
A. Yes, the reaction will stop by itself because the rate of product formation is saturated.
B. Yes, the reaction will be over quickly because rate of product formation is large.
C. No, the reaction could be an explosion, due to the exponential increase of the formation of product.
D. No, the reaction has likely slowed down quickly, and so there is little to observe in the reaction.
5. What is the rate law of the following reaction, given the data provided below?
CH3I + Cl- → CH3Cl + I-
(This is an example of an SN2 reaction, which have encountered (or will encounter) in your organic chemistry class.)
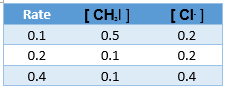
A. R = k [ CH3I ]
B. R = k [CH3Cl ]
C. R = k [ Cl- ]
D. R = k [ CH3I ][ Cl- ]
E. R = k [ CH3Cl ][ Cl- ]
Answers:
-
A: The rate equation for a zero order reaction has no factor corresponding to concentration.
-
B: The rate constant is independent of C-14 concentration, but the rate does depend on the concentration of C-14.
-
E: Both the rate constant and rate of reaction decrease for a catalyzed reaction.
-
C: The rate of product formation is increasing exponentially, so if the product was a gas, then the resulting rapid increase in the volume of gas would be dangerous.
- D: Doubling either methlyiodide or chloride ion will double the rate.
Citations:
[1] UCDavis Chemwiki. The Rate Law.
http://chemwiki.ucdavis.edu/Physical_Chemistry/Kinetics/Rate_Laws/The_Rate_Law (accessed 11/10/14)
[2] UCDavis Chemwiki. Elementary Reactions. http://chemwiki.ucdavis.edu/Physical_Chemistry/Kinetics/Rate_Laws/Reaction_Mechanisms/Elementary_Reactions (accessed 11/10/14)
[3] Purdue Chemistry. Rate Laws from Graphs of Concentration Versus Time. http://www.chem.purdue.edu/gchelp/howtosolveit/Kinetics/IntegratedRateLaws.html (accessed 11/10/14)
[4] HyperPhysics. Carbon Dating. http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/cardat.html#c1 (accessed 11/10/14)
[5] Atkins, P. W., and Julio De Paula. Atkins' Physical Chemistry. Oxford: Oxford UP, 2006. Print.\
[6] UCDavis Chemwiki. Transition State Theory. http://chemwiki.ucdavis.edu/Physical_Chemistry/Kinetics/Modeling_Reaction_Kinetics/Transition_State_Theory/Transition_State_Theory (accessed 11/10/14).
[7] ChemGuide. Rate Constants and the Arrhenius Equation. http://www.chemguide.co.uk/physical/basicrates/arrhenius.html (accessed 11/24/14).
[8] UCLA Chemistry. Illustrated Glossary of Organic Chemistry: Transition State. http://www.chem.ucla.edu/harding/IGOC/T/transition_state.html (accessed 11/24/14).
[9] Lecture 38: Chemical Principles. Professor Dominika Zgid. November 24,2015. Slide 24
Comments (0)
You don't have permission to comment on this page.