Thermodynamics is concerned with the relationship of heat, work and other macroscopic properties. It is based on the average of the microscopic behavior of molecules and therefore called statistical mechanics.
This site focuses on ideal gas systems and how work and heat change when the systems, initially in equilibrium, are subject to a change. We will focus on isothermal, adiabatic and quasistatic processes.
Ideal Gas Law
The Ideal Gas Law describes the relationship between pressure, volume, number of moles of a gas, and temperature in an ideal gas. An ideal gas is one with molecules of a negligible volume with negligible interactions between them. Real gases are approximated as ideal gases in order to simply relate pressure, volume, number of moles, and temperature.
PV=nRT (The Equation of the Ideal Gas Law. By convention, P = pressure in Pascals, V=volume in m3, n= number of moles, R= Ideal gas constant, 8.3145 J/mol*K, T= temperature in Kelvins) (Another common value of R is 0.08206 L*atm/mol*K, for pessure in atm, volume in l and temperature in K)
In expansion and compression work, volume is changing, and the ideal gas law allows us to relate this change to the other properties of the gas.
Work
Work is known to most students to be force times change in distance. Distance is changing, affected by a force, and therefore work is
W= F∆d
In compression and expansion work, the volume is changing, affected by a pressure.
W= P∆V
Work is a path-dependent function. The process by which work is done changes the final value, unlike a state function, in which path does not change the final value. Whether the work is done reversibly or irreversibly determines how it is calculated. Work is done reversibly when the changes in volume are infinitesimally small, or the work is done in an infinite number of stages.

Figure 1. An image describing irreversible and reversible work. Reversible work is shown as being done in infinite, infinitesimally small stages.
Expansion Work
A system does expansion work when volume increases (expands) against an external pressure. When the internal pressure is greater than the external pressure, volume increases.
In an expansion, work is done by the system on the surroundings.
Compression Work
A system is compressed when work is done by the surroundings on the system. In this case, the external pressure is greater than the internal pressure, and volume decreases.
For this class, work is positive when done on a system, and negative when done by the system.
Work done on the system is done by the surroundings, and work done by the system is done on the surroundings.
Work done on system= Wsys (positive by convention)
Work done on surroundings = Wsurr (negative by convention)
Wsys= -Wsurr

Figure 2. Image displaying Expansion and Compression work in a simple system.
Heat
Heat is defined as a process of increasing or decreasing the energy contained in an atom or molecule. Heat is conceptualized by a “flow” always flowing from high temperature to low temperature.
q=Mcs∆T
Heat is proportional to temperature change, related by a factor called “heat capacity, cs, and mass. Changing the temperature of a large mass requires more heat, because more material must be affected.
When heat is transferred into the system, heat is positive. When it is transferred out of the system, it is negative.
Heat transferred into the system must be removed from the surroundings, and heat transferred out of the system must be transferred into the surroundings.
Heat transferred into system = qsys
Heat transferred into surroundings = qsurr
qsys= -qsurr
Internal Energy
Internal energy measures the energy of molecules or atoms. The symbol for internal energy is U.
Molecules have potential energy arising from interactions with other molecules. Molecules attract and repel each other, and the strength of these interactions are based upon the relative locations of molecules.
Molecules also have rotational and vibrational energies, which account for the movement of electrons in an atom or molecule.
Molecules are constantly moving, and therefore have kinetic energy. When molecules collide, they exchange kinetic energy. The distance a molecule travels before undergoing a collision with another molecule is the Mean Free Path. The kinetic energy of molecules is determined by temperature. When temperature increases, kinetic energy of molecules increases, and therefore internal energy increases.
Internal energy is therefore affected by heat and work, since the energy of a molecule changes as work is done and heat is exchanged.
Thus, ∆U = q+W
Enthalpy
Enthalpy measures the total energy of a system, incorporating internal energy and energy of pressure and volume. Enthalpy changes when the internal energy increases or decreases and/or work is done on or by the system.
At constant pressure: H(Enthalpy)= U + PV
Since qp = ∆U +P∆V
qp = ∆H
When pressure is changing, change in enthalpy can be calculated as
∆H = ∆U + ∆(PV)
Isothermal process
In the isothermal process the temperature is held constant meaning that ΔT=0. In order for this to occur the system exchanges heat with the surrounding, so that heat does not affect the kinetic energy of the molecules and therefore the internal energy of the system. Thus, the change of internal energy of a system is proportional only to the change in temperature, as seen in the equation above, and we can conclude that for isothermal processes, ΔU=0.
Furthermore, the change in enthalpy of a system is also only depended on the change of temperature, so that ΔH=0.
The First Law of Thermodynamics states that
ΔU=w+q
where ΔU is the change of internal energy, w is the volume-pressure work done by the gas and q is the heat transferred from the system.
Since, ΔU=0 for isothermal processes, we can conclude that w=-q.
Note that w is the pressure-volume work done by the gas and also the area under the curve of a pressure-volume graph. But for reversible isothermal processes, we cannot use the simple equation w=-PΔV, since the pressure is not constant in this process. Thus, we can infer that the work done by the gas equals to the sum of the pressure at a determined time times δV. This results in the following equation:

An example of a graph of this process is given below. The area under the curve equals to the work done by the gas and the heat exchanged with the surrounding. Note that in order to keep the temperature constant, the volume and the internal pressure of a system have to change.

Figure 3. PV graph of reversible isothermal process and its work
Adiabatic process
In the adiabatic process there is no exchange of heat between the system and the surrounding. This is accomplished by isolating the system with adiabatic walls (walls that do not allow heat transfer) and changing the volume, pressure and temperature of the system.
Since, the heat is constant, q=0 and ΔU=w, where q is the heat exchanged between a system and its surroundings, ΔU is the change of internal energy of that system, w is the volume-pressure work done by the gas of the system.
Also, as seen previously in this site, ΔH=ncpΔT, where ΔH is the change in enthalpy of the system, n is the number of moles of gas present in the system, cp is the heat capacity of the gas at constant pressure and ΔT is the change in temperature.
For a reversible process, we can also write these equations as:
ΔU= ncvΔT=w and w=-PΔV
Where P is the internal pressure of the system, ΔV is the change in volume of the system, cv is the heat capacity of the gas at constant volume and n is the number of moles of gas present in the system.
Thus, dU= ncvdT and w=-PdV at a specific point in the pressure-volume graph.
For the adiabatic process ΔU=w, where ncvdT=-PdV at a specific point in the pressure-volume graph. Substituting the ideal gas law in this equation, while using cp-cv for R, and simplifying it, we get:

We can call further simplify this by setting γ=cp/cv
Adding all these we obtain:

By solving this equation we conclude that:
 and
and 
The work done by the system is again equal to the area under the curve (Figure 4).

Figure 4. Work done on adiabatic process
The equation and the graph tell us that as the volume increases (the system does work), the temperature decreases (molecules lose kinetic energy). The opposite is also true for decreasing volume.
The relationship of the graphs is that the adiabatic process curve falls more quickly than the isothermal process curve. The following problem can be easily solved by following this relationship between the two graphs.
Two identical bubbles of gas form at the bottom of a lake, then rise to the surface. Because the pressure is much lower at the surface than at the bottom, both bubbles expand as they rise. However, bubble A rises very quickly so that no heat is exchanged between it and the water. Meanwhile, bubble B rises slowly (impeded by a tangle of seaweed), so that it always remains in thermal equilibrium with the water (which has the same temperature everywhere). Which of the two bubbles is larger by the time they reach the surface? (problem 1.38 in Thermal Physics, Daniel Schroeder)
As the initial and final pressures are equal for both bubbles and the initial volume is also the same, we have to imagine, where in the graph the bubbles at the end of the isothermal and adiabatic processes will be in relation to one another. Since bubble A is reaching the surface first through an adiabatic process, it will reach the final pressure first and therefore the volume will be larger than the one reached by bubble B that will reach the final pressure later by following an isothermal process. Therefore bubble B is bigger than bubble A, when it reaches the surface of the lake. The graph below shows this relationship.

Figure 5. Relationship between Pressure and Volume in an adiabatic and an isothermal process
Quasistatic Process
Quasi static
seemingly/almost with little or no change
A quasistatic process in thermodynamics refers to a process carried out in a time-scale much longer than the relaxation time of a system that the system seems to be remaining in its equilibrium. Keeping in mind that the relaxation time is the time needed for a system to return to its equilibrium after being suddenly disturbed, we can infer that in a time-scale much longer than the relaxation time, the system would have returned to its equilibrium, seeming to have undergone no change.
One important thing about quasistatic process is that they are frequently mistaken as reversible process. In fact, reversible processes are all quasistatic -- they come from infinitesimal change in the surrounding with no entropy production. For example, recall from the lecture that in a reversible isothermal process, external pressure only has a slight difference (which can be neglected) from the pressure of the system, and therefore Pext=P±dP≈P. This equation shows how the difference between external pressure and internal pressure is infinitesimal, and therefore they are almost close to the equilibrium between the two.
An example of a reversible process would be having two people with same weight on each sides of a see-saw and adding a few grains of sand on one of the sides. This infinitesimal change will cause the see-saw to tilt in the direction of the heavier side. Adding another few grains of sand on the other side will cause the see-saw to tilt to the other side. As can be seen in the example, in reversible processes, infinitesimal change determines the direction of the process.
However, all quasistatic processes are not necessarily reversible. If there is heat flow in/out of the system or entropy is created, the system is irreversible although it may be quasistatic. For example, imagine a tire with a small hole and air leaking out of the tire at a very slow rate. If it were a reversible process, the direction of the process would have to be reverted, meaning that air should go back into the tire, if we blow against the leak to slightly increase the outside pressure. However, a hole in the tire creates an entropy, a large driving force for the air to leak out until the internal pressure of the tire gets lower than the external pressure. Another example would be the work of a piston subject to friction. When piston is pushed along a wall with friction, some of the system’s energy is lost through heat, and that lost energy by heat will not be recovered even though the piston comes back to its original place. Therefore, the relationship between quasistatic and reversible process, simply put, will be as shown in Figure 6.

Figure 6. Venn diagram showing relationship of quasistatic process and reversible process
Quasistatic Process and Work
Formulas for work in a quasistatic process with some constant variables can be largely divided into three:
 (basic formula for work)
(basic formula for work)
1. Constant pressure: Isobaric processes,

When pressure is held constant, since P1=P2= P / P2*V2-P1*V1=P(V2-V1).
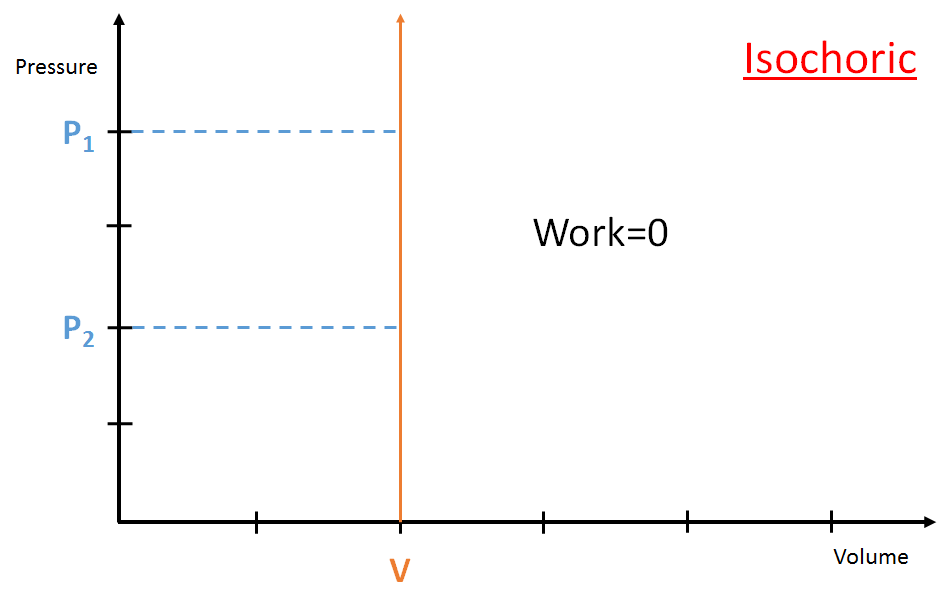
2. Constant volume: Isochoric processes,

When volume is held constant, the work is 0 because dV=0.
3. Constant temperature: Isothermal processes,


Below are the graphs that show the relationship between volume, pressure, and work under each conditions:


(a) (b) (c)
Figure 7. Graph of Volume vs Pressure and their work under three types of quasistatic process: (a) isobaric, (b) isochoric, and (c) isothermic.
Calculating Work from Pressure-Volume Graph
Keeping in mind the relationship between volume and pressure and its work in the graph, let us think about a monatomic ideal gas constrained by a piston during a cyclic process shown below (Figure 8.a). We can infer from the graph that there will be no change in the position of the piston where volume is constant (at B and D). At A, the volume is increased, and at C, the volume is decreased, so at point A and C, the pistons will move. Work done on the gas can be calculated with the below process.
(a) 

(b)
Figure 8. (a) The PV graph of a monatomic ideal gas of example constrained in the piston undergoing a cylic process. (b) Process of calculating the work of the gas from (a).
At A and C where the volume is constant (isochoric), WA=WC=0. At B, work done is positive with equation WB=P2(V2-V1). At D, work done is negative with equation WD=P1(V1-V2). Total work done is the addition of all work done on the gas. Therefore, WA+WB+WC+WD=WB+WD= area inside the rectangle (Figure 8.b).
Concept Questions:
1) Explain why the change in internal energy and the change in enthalpy are 0 during an isothermal process.
2) What is the relationship between the graphs of an isothermal process and an adiabatic process?
3) True/False?
a_All reversible processes are quasistatic processes.
b_All quasistatic processes are reversible processes.
Answers:
1) The change in internal energy, as well as the change in enthalpy, is proportional to the change in temperature, which in an isothermal process is 0.
2) Since the temperature does not change in the isothermal process, the reversible isothermal process corresponds to an isotherm. In the adiabatic process, heat is constant and therefore the reversible process goes from one isotherm to another, representing the temperature change as well as the changes in volume and pressure. Thus, the slope of the adiabatic process is steeper than the one for the isothermal process.
3) a_True. The change in the reversible processes are so infinitesimal that the system stays in its equilibrium. Therefore, they all are quasistatic, which seems to stay in its equilibrium.
b_False. Quasistatic process "seem" to be in its equilibrium simply because it happens in a time-scale longer than the relaxation time. If there is heat flow or entropy is created in the quasistatic process, it cannot be reversible.
References
Oxtoby, D. W.; Gillis, P. H.; Campion, A. Introduction to Thermodynamics and Kinetics. 7th edition. Mason: Cengage Learning; 2011
http://www.ims.uconn.edu/~rjh/MSE3001_10/Handout10.pdf
http://learnthermodynamics.blogspot.com/2011/10/quasi-static-process.html
Comments (0)
You don't have permission to comment on this page.