The Beginnings of Quantum Mechanics
Classical Mechanics
In the seventeenth century, the work of physicists such as Galileo Galilei and Isaac Newton inspired and triggered many other experimental and theoretical science works which later on developed into classical mechanics. Classical mechanics are fundamental laws of physics that enables the prediction of motions of particles based on assumptions that energy values are continuous. It was thought to be applicable for motions of any objects - from electrons to planets. Through classical mechanics, one can make predictions of the future deterministic “position” of a group of particles given their current position, velocities, and forces on them, also accounting for unknown forces. It was not until the 20th century that the classical mechanics was proved not to be applicable in certain cases.
Max Planck & Black Body Radiation
Max Planck achieved great insight about energy while studying new experiments on the interactions of solid objects with radiant energy, known as blackbody radiation (see the next section Black-body radiation).
According to classical physics, the sources of black body radiation are oscillating electric charges on the surfaces of objects that have been accelerated by thermal motion. The motion of the oscillating charges for a certain period produces radiation whose frequency is inversely related to that period. Many scientists have used this knowledge to map the radiation intensity curve, as shown by the “classical” curve in Figure 1. However, this model disagrees greatly with experimental results at high frequencies, which is the result based on the Rayleigh-Jeans law. This inconsistency with the experiment is called the “ultraviolet catastrophe,” where according to the classical mechanics law (Rayleigh-Jeans law) at large frequencies, the radiation intensity approaches infinity.

Figure 1. Spectral irradiance graphs as a function of frequency and wavelength. This shows the ultraviolet catastrophe as well as the formulas relevant to Rayleigh-Jeans and Planck’s law.
In attempts to explain the experimental results, Planck first hypothesized that electromagnetic oscillators are limited to discrete energy values, unlike in classical physics where energy is continuous and has no restriction to the value of the total energy. Next, Planck predicted the radiation intensity curve by calculating the average energy of the quantized oscillators at each frequency as a function of temperature. Planck hypothesized that excitation of a particular oscillator is an all-or-nothing event based on whether there is enough thermal energy to cause oscillation or not.
On the basis that energy is quantized and that the electromagnetic frequency v are integer multiples of hv, Planck derived what is now called the Planck distribution, which is shown in Figure 1.
The quantum approach (Planck’s law) provides a very accurate representation of how black-body intensity relates to wavelength, where at each temperature measurement, a corresponding maxima shows what type of radiation is produced given a certain criteria.
Black-body Radiation
One of the problems with the classical mechanics was brought up through what is called the black-body radiation. It is characterized as an emitted radiation from matter that is perfectly dark in nature that can absorb all electromagnetic radiation from the environment, meaning the object is perfectly non-reflective. This body is also considered to be thermodynamically at equilibrium, this means that there are no net phase changes or energy transfers with the environment. Since this body is non-reflective, that means that it absorbs all radiation that it encounters and all emissions from this black-body are oscillating charges that create the electromagnetic wave that this body emits. The black-body emits an infrared radiation, which is invisible to the naked eye. Currently, there are no examples of a perfect black-body; there are only close representations that approximately display the properties of a black body. Two examples are graphite and carbon black. Another example to consider is a furnace with a very small hole. This furnace is able to absorb any type of electromagnetic radiation that is able to be input to this system, and it will stay largely trapped inside the furnace’s black walls, meaning it has been absorbed. Afterwards, there might be moments where some radiation escapes the furnace to represent radiation that is emitted by the black body. This idea was proposed by Gustav Kirchhoff in 1860, but was further developed by Rayleigh-Jeans and Planck. The former used a classical physics approach, while the latter took a different approach that led to what is currently known as quantized approach. These approaches used different formulas to map out the radiation intensity as a function of wavelength. The Rayleigh-Jean's law intended to describe spectral radiance of electromagnetic radiation at all wavelengths from a black-body at a given temperature.
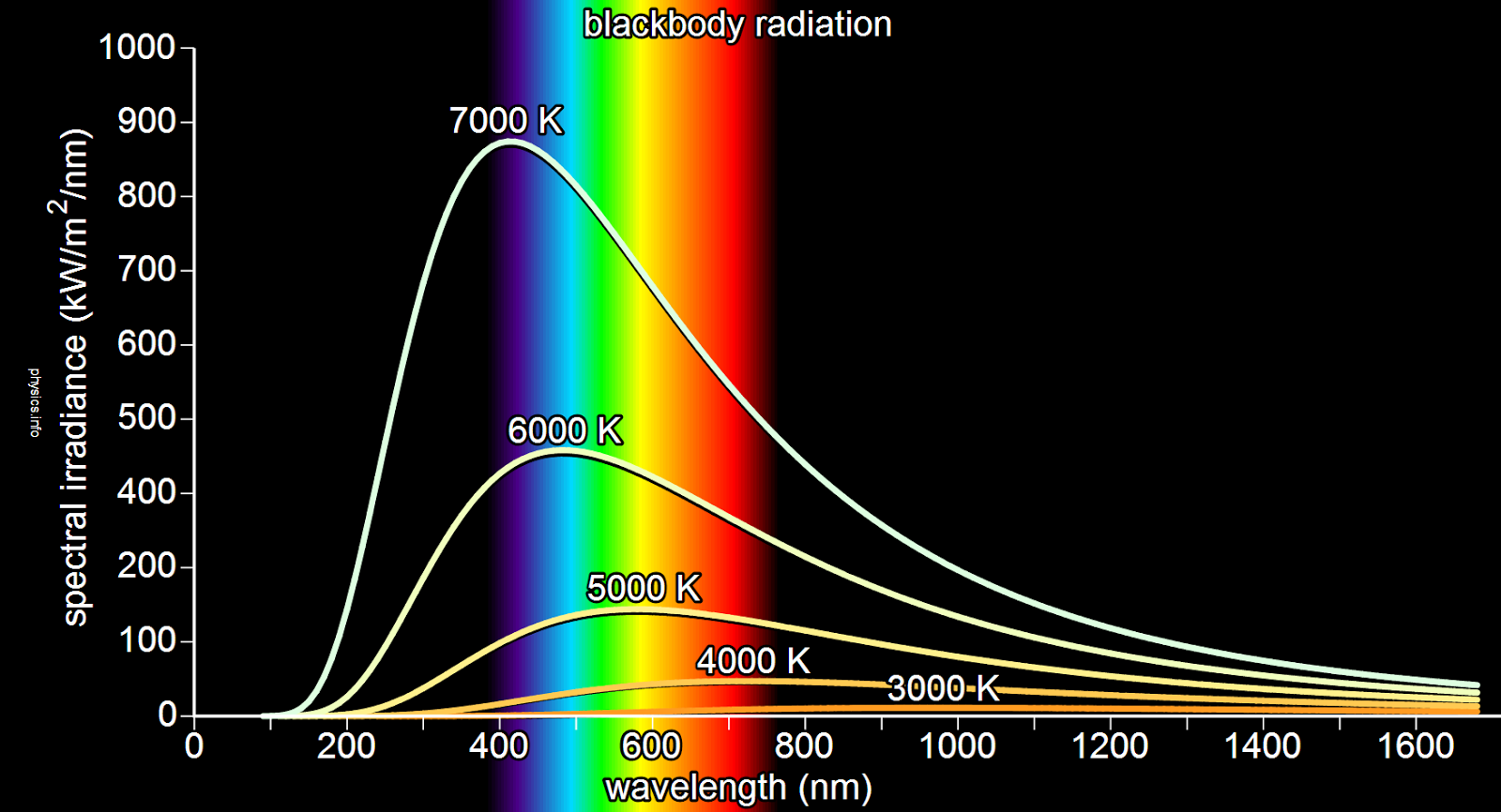
Figure 2. Spectral irradiance graphs as a function of frequency and wavelength. This shows the different colors along the visible spectrum that can be observed at different temperatures and wavelengths.
As stated before, different intensities of radiation are released from an object depending on the wavelength of the radiation. It should be noted that at different temperatures, there are distinct peak that show what color is typically shown at a certain temperature at different wavelengths, which is shown in figure 2.
The Wien’s Displacement formula is as follows:

Figure 3. Wien’s Displacement formula. Used to solve for radiation intensity.
This formula is another version of Planck’s law. h is Planck's constant (Js), f is the frequency of the emitted radiation (Hz), c is the speed of light (m/s), T is the temperature (K), λ is wavelength (m), and k is the Boltzmann constant (J/K). However, this set of equations explicitly solves for the radiation intensity at certain temperatures and frequencies or wavelengths. There are two ways to express radiation intensity at a given temperature: either with wavelength or frequency. The units of the intensity, based on which formula used, is given and used depending on which values that are needed to be solved. Figures 1 and 2 show the spectral irradiance based on several different temperatures.
The failure of classical physics is attributed to the fact that there is a certain point, called the classical limit, where classical mechanics cannot account for activity in nature and a shift to quantum mechanics is required to better calculate the properties that these objects exhibit.. If the time and energy scales of a system of interest are ∆t and ∆E, respectively, than classical physics will be valid when ∆E×∆t>>h (the so called classical limit). In contrast, once ∆E×∆t∼h , which is typically the case on the atomic and subatomic scale, classical physics will no longer be valid and will need to be replaced by quantum mechanics, which is how Planck addressed the problem that Rayleigh-Jeans had in his proposed solution to the black-body problem.
Photoelectric effect
Photoelectric effect was another problem in which there was failure with the application of classical mechanics. Photoelectric effect was brought up by the observation that light causes electrons to be ejected from a metal’s surface, thereby resulting in a flow of electric current. Since classical physics described light as wave, the electrons were thought to break away from the surface by oscillating with the light wave. This behavior of electrons was thought to be intensity-dependent: the larger the intensity, the larger the amplitude, the more electrons ejected, and the more kinetic energy. However, it was proved that the electrons’ behavior depends primarily on the frequency of light, and on intensity after the condition is met for the threshold frequency. There was no flow of photocurrent below the metal’s unique threshold frequency regardless of the intensity. Once the electrons were excited by radiation of frequency above the threshold, the total current of photoelectrons emitted was proportional to the radiation intensity. Simply put, threshold frequency is the minimum condition for photoelectrons to be emitted and intensity is what ultimately defines the total current of the photoelectrons (Figure 4).

Figure 4. Photoelectric effect depends both on frequency and intensity. Only light above the threshold frequency results in photocurrent. Above the threshold, photocurrent depends on the intensity of light, not on the frequency.
Regarding the maximum energy of the electron, the total energy of electrons emitted is proportional to the frequency of light (Figure 5). The energy of electrons is quantized into quanta of energy called photons (quantization of electromagnetic energy), and the energy of each photon is proportional to the frequency of light and can be written as E=hv, where h is Planck’s constant. Only one photon is needed to excite the surface and emit the electrons. That being said, the intensity which determines how many photons are in radiation, does not affect the maximum energy. This outcome contradicted the expectation of early scientists because according to classical electromagnetic theory, the energy associated with electromagnetic radiation should only depend on the intensity of radiation.

Figure 5. The maximum kinetic energy of the ejected electrons is proportional to the frequency of the light, regardless of the intensity.
Below is a simulation of photoelectric effect. You can see by changing the intensity and wavelength that however strong the intensity is, no electric current flows above a certain wavelength; that is, below the threshold frequency since wavelength is inversely proportional to frequency. Above a certain wavelength, however, there is more flow of current with the increase of intensity. Also, by changing the targets, you can see that each target has different threshold frequency values. For example, light around wavelength of 450nm causes photoelectric current from sodium but not platinum, meaning that sodium has a much lower threshold frequency compared to platinum.
Einstein
Einstein was the first to introduce the quantization of electromagnetic energy, which he submitted to the “Annalen” in one of five revolutionary papers. Planck had only assumed that electromagnetic energy came in finite amounts while developing his law of black-body radiation, E=hv. But Einstein was able to explain the quantization of light energy using the Wien’s law. First, Einstein derived from Wien’s law a corresponding entropy based on the high frequency limit.This entropy would equal the entropy a group of non-interacting point-like particles with energy E=hv. Einstein realized that this characteristic of light must be assumed in order to explain many contemporary experiments. These particles were given the name of “photons” about 20 years later, and the idea of the wave-particle duality of photons would eventually lead towards the development of the theory of relativity.
Concept Questions:
1. Why are there no perfect representations of perfect black-bodies?
2. According to the Wien Displacement law, the maximum wavelength of black body radiation increases as temperature (increases or decreases).
3. Light of unknown property was shone onto surface of two different metals (metal A and metal B), but only metal B had current of photoelectrons. What difference between the two metals contributes to the result?
Answers:
1. There are no perfect representations because a perfect black-body means that it completely absorbs other electromagnetic radiation (meaning it is nonreflective) whilst radiating its own specific radiation at a given temperature. There are no such objects that perfectly have this property and we can only come so close with approximate black-body objects. Black holes are also a very close representations to black-bodies.
2. Decreases - the Wien displacement law shows that there is an inverse relationship between the peak wavelength and temperature. Although the wavelength distribution shape will be the same for any temperature, the average thermal radiation depends only on the ratio of 1/T.
3. Metal B has a threshold frequency lower than the frequency of the light shone and metal A has has a threshold frequency higher than the frequency of the light shone.
References:
"Albert Einstein as the father of solid state physics." Arxiv. N.p., n.d. Web. 13 Sept. 1920. <http://arxiv.org/abs/physics/0508237>
Atkins, P. W., and Julio Paula. "Quantum theory: introduction and principles." Atkins' Physical chemistry. 8th ed. New York: W.H. Freeman, 2006. 243-250. Print.
Daniel C. Harris. Quantitative chemical analysis. W. H. Freeman and Co. 8th ed, 2010
"Blackbody Radiation - The Physics Hypertextbook." The Physics Hypertextbook. N.p., n.d. Web. 20 Sept. 2013. <http://physics.info/planck/>
"Black Body Radiation." Eggles Cliffe. N.p., n.d. Web. 20 Sept. 2013. <www.egglescliffe.org.uk/physics/astronomy/blackbody/bbody.html>
"Blackbody Radiation." Hyper Physics. N.p., n.d. Web. 20 Sept. 2013. <http://hyperphysics.phy-astr.gsu.edu/hbase/mod6.html>
“PhysicsLAB: Famous Discoveries: The Photoelectric Effect.” Physics Lab. N.p., n.d. Web. 20 Sept. 2013. <http://dev.physicslab.org/Document.aspx?doctype=3&filename=AtomicNuclear_PhotoelectricEffect.xml>
Comments (0)
You don't have permission to comment on this page.